
안녕하세요. 스마트컨트렉트 개발자 개발이 체질의 최원혁입니다.
이번 게시글에서 소개해드릴 내용은 2진수의 4칙연산입니다. 2진수(binary digit)는 비트를 뜻하는 말로 컴퓨터에서 사용되는 데이터의 최소 단위이며, 주로 Low-level 언어에서 사용하는 데이터 최소 단위입니다.
우리가 흔히 사용하는 숫자는 10진수라고 불리며, 10진수만의 규칙에 의한 4칙연산을 통해 계산합니다. 2진수 또한 2진수만의 규칙에 의해 4칙연산이 진행됩니다.
2진수를 활용한 연산을 익히게 되면 알고리즘을 개발할 때 시간 복잡도가 훨씬 낮은 로직을 구현할 수 있습니다. 스마트 컨트랙트를 개발하게 되면, 로직의 시간 복잡도에 따라 가스비가 다르게 측정되기 때문에, 2진수 연산을 활용한 알고리즘을 스마트 컨트랙트에 적용하게 되면 굉장히 최적화된 로직을 구현할 수 있는 개발자가 될 수 있습니다.
2진수 계산 규칙 :
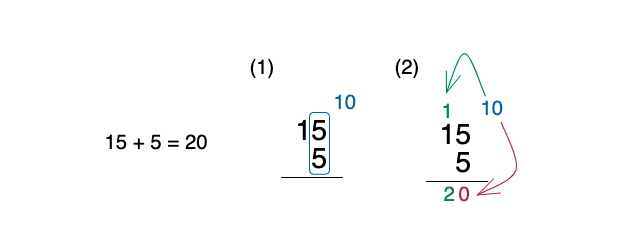
우리가 흔히 사용하고 있는 10진수는 위와 같이 익숙한 형태로 되어 있습니다. 이 처럼 10진수는 두 수의 합이 10이 되면 1의 자리 숫자만 남기고 나머지 숫자는 다음 더하기로 넘겨줍니다.
- 10진수 -> 10일때 올림
- 2진수 -> 2일때 올림
이때, 10이상의 숫자를 넘겨주는것 처럼 2진수는 2이상의 숫자를 넘겨주면 됩니다.
2진수와 10진수 :
2진수에서 10진수로 변환하는 방법에 대해서 아래 링크를 참고해주세요.
[Solidity] 비트마스크(BitMask) 연산 || Solidity 0.8 | Operators ||
안녕하세요. 스마트 컨트렉트 개발자 개발이 체질의 최원혁입니다. 이번 게시글에서 Solidity에서 활용할 수 있는 비트마스크(BitMask) 연산에 대해 알아보겠습니다. 비트마스크(BitMask) 란? 10진수를
borntodevelop.tistory.com
2진수의 더하기 :
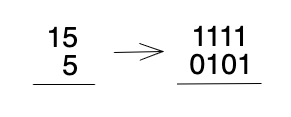
15 + 5를 예로 설명해보겠습니다.
[15 + 5]를 2진수로 표현하면 [1111 + 0101]로 표현할 수 있습니다.
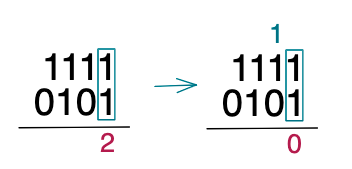
10진수와 마찬가지로 1의 자리 숫자부터 연산을 시작합니다. 1+1은 2가 되며, 2진수의 규칙에 따라, 2는 다음 숫자에 1을 넘겨주고, 0이라는 결과를 내려줍니다.
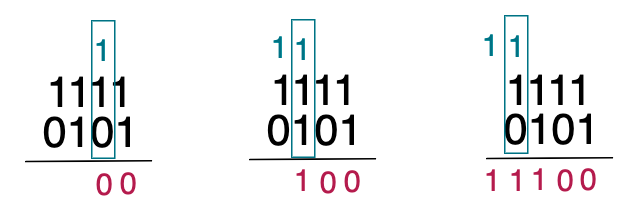
두번째 연산에서 념겨 받은 1을 같이 더하면 2가 됩니다. 다시 2진수의 규칙에 따라 1을 다음숫자로 넘겨주고 0이라는 결과를 내립니다. 이 과정을 반복하면 최종적으로 결과는 11100됩니다.
- 15 + 5 = 20
- 1111 + 0101 = 11100 => 20
마지막으로 2진수 결과를 10진수로 바꾸면 같은 결과임을 확인할 수 있습니다.
2진수의 빼기 :
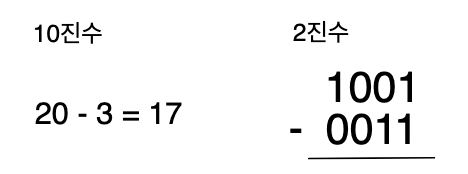
20 - 3를 예로 설명해보겠습니다.
[20 - 3]를 2진수로 표현하면 [1001 - 0011]로 표현할 수 있습니다.
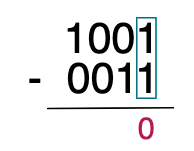
마찬가지로 1의 자리 숫자부터 연산을 시작합니다. 1과 1를 빼면 0이니까, 바로 답을 내릴 수 있습니다.
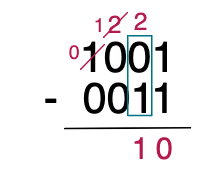
두번째 자리 숫자 0-1를 뺴기하려고 하니, 마이너스 숫자가 나와서 계산을 못합니다. 이런 경우, 우리는 옆에 자리 숫자에서 숫자를 빌려와 계산합니다.
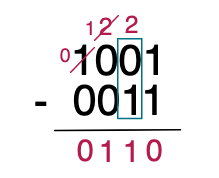
이 과정을 반복하면 최종적으로 결과는 0110됩니다.
- 20 - 3 = 17
- 1001 + 0011 = 0110 => 17
마지막으로 2진수 결과를 10진수로 바꾸면 같은 결과임을 확인할 수 있습니다.
2진수의 곱하기 :

9 x 3를 예로 설명해보겠습니다.
[9 x 3]를 2진수로 표현하면 [1001 x 0011]로 표현할 수 있습니다.
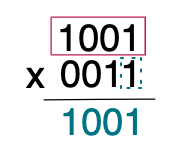
곱하기는 1의 자리 숫자(1)와 곱하는 대상의 숫자(1001)를 모두 곱해서 결과로 내립니다.
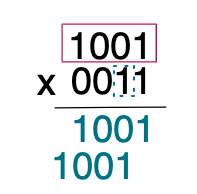
그 다음 숫자와 곱하는 대상의 숫자 모두를 곱한 후, 위 사진처럼 한간 띄고 결과를 내립니다.
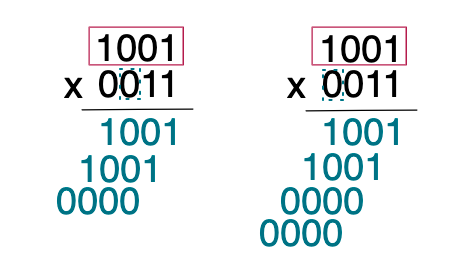
이를 반복하여 모든 숫자를 전부 곱합니다.
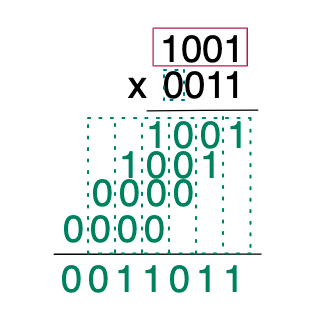
이후, 각 위치에 있는 숫자들을 전부 더해서 내려주면 최종적으로 결과는 11011이 됩니다.
- 9 x 3 = 27
- 1001 x 0011 = 0011011 => 27
마지막으로 2진수 결과를 10진수로 바꾸면 같은 결과임을 확인할 수 있습니다.
2진수의 나누기 :

9 ÷ 3를 예로 설명해보겠습니다.
[9 ÷ 3]를 2진수로 표현하면 [1001 ÷ 0011]로 표현할 수 있습니다.
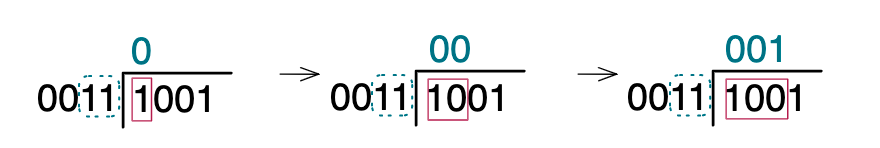
나누기 또한 10진수의 나누기와 똑같습니다. 나누고자 하는 숫자(11)가 나눠지는 숫자(1)보다 크면 나눌 수 있는 숫자가 없으니 옆으로 한칸 옮겨 자리수를 늘립니다. 다음칸 또한 나누고자 하는 숫자(11)가나눠지는 숫자(10)보다 크면 나눌 수 있는 숫자가 없으니 다시 한번 옆으로 한칸 옮겨 자리수를 늘립니다.
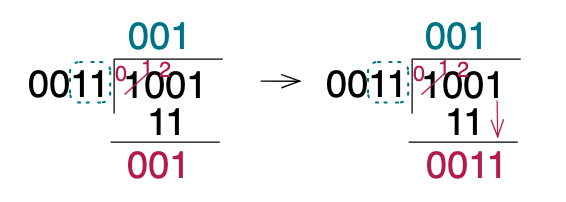
나눠지는 숫자(100)가 나누고자 하는 숫자(11) 보다 커졌으니, 이제 연산을 할 수 있습니다. 2진수로 100 - 011은 001이기에 값을 내려줍니다. 이 후, 나머지 1을 내려 0011을 만듭니다.
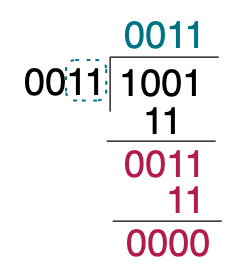
0011과 0011을 빼면 값은 0이 나오면서 최종적으로 나누기의 결과 0011이 됩니다.
- 9 ÷ 3 = 3
- 1001 ÷ 0011 = 0011 => 3
마지막으로 2진수 결과를 10진수로 바꾸면 같은 결과임을 확인할 수 있습니다.
지금까지 2진수 4칙연산(더하기,빼기,곱하기,나누기)에 대해 알아봤습니다.
감사합니다.
'IT Series' 카테고리의 다른 글
| [확률과 통계] 순열(permutation) 이해하기 (with example) (0) | 2025.01.31 |
|---|---|
| [확률과 통계] 합의 법칙과 곱의 법칙 이해하기 (0) | 2025.01.30 |
| [IT Series] 컴퓨터의 I/O와 인터페이스 CLI,GUI (0) | 2022.07.08 |
| Smart Contract Best Practices Revisited: Block Number vs. Timestamp 재검토된 스마트 계약 모범 사례: 블록 번호 대 타임스탬프 (0) | 2022.05.18 |
| IT지식 ) 컨텐츠 주소 지정 저장소(CAS) (0) | 2022.04.29 |

댓글