
안녕하세요. 스마트컨트렉트 개발자 개발이 체질의 최원혁입니다.
이번 게시글에서 소개해드릴 DeFi Series는 Uniswap V3 업데이트의 핵심 집중화된 유동성(Concentrated Liquidity)입니다.
기존의 Uniswap은 두 가지 암호화폐를 거래할 수 있는 거래의 장을 형성하여 CPMM 함수로 자동으로 거래가 이뤄지는 AMM 방식의 거래 구조를 구현했습니다.

하지만 CPMM 함수는 구매자가 의도했던 가격과 실제 거래 가격 사이에 차이가 발생하며 구매자의 손해를 보는 일이 발생했습니다. 이런 현상을 슬리피지라고 하며, 슬리피지는 유동성 풀의 규모가 작은 곳에서 특히 심하게 발생했습니다.
이런 문제점을 Uniswap V2의 게으른 유동성(Lazy Liquidity)이라고 합니다.
Uniswap V3는 이러한 고질적인 문제를 해결하기 위해 집중화된 유동성(Concentrated Liquidity)이라는 유동성 공급 방식에 변화를 주어 문제를 해결하기로 했습니다.
📌 DEX 기본 개념과 Uniswap V2의 게으른 유동성(Lazy Liquidity)에 대한 내용은 아래 게시글을 참고해주세요.
Uniswap 기본 기념 파헤치기
[DeFi Series] Uniswap 기본 개념 파헤치기 || DEX | AMM | CPMM | Liquidity | Slippage | LP Token ||
안녕하세요. 스마트컨트렉트 개발자 개발이 체질의 최원혁입니다. DeFi Series로 소개해드릴 내용은 Uniswap 기본 개념입니다. Uniswap은 암호화폐 시장의 대표적인 탈중앙화 거래소이며, Uniswap이 만들
borntodevelop.tistory.com
Uniswap V2 : 게으른 유동성(Lazy Liquidity)
[DeFi Series] Uniswap V2 게으른 유동성(Lazy Liquidity) || Math | DeFi ||
안녕하세요. 스마트컨트렉트 개발자 개발이 체질의 최원혁입니다. 이번 게시글에서 소개해드릴 DeFi Series는 Uniswap V2 게으른 유동성(Lazy Liquidity)에 대해 알아보겠습니다. 게으른 유동성(Lazy Liquidit
borntodevelop.tistory.com
(1) Uniswap V3 집중화된 유동성

기존의 유니스왑 V2의 공식에서 V3의 공식은 위와 같이 변화하였습니다. 특히 새로운 변수 Pa(최솟값)와 Pb(최댓값)를 볼 수 있습니다. 집중화된 유동성은 유동성 공급자가 공급하고자 하는 유동성의 최대치와 최소치를 설정할 수 있게 업데이트되었습니다.
지금부터 유니스왑 V3 Whitepaper에 나와있는 집중화된 유동성 CPMM을 예시와 함께 수학적으로 이해해 보겠습니다.
Example
현재 유동성 제공자가 MTK/USDC 유동성 풀이 형성하였습니다.
- X : MTK/USDC 유동성 풀의 MTK 현재 공급량
- Y : MTK/USDC 유동성 풀의 USDC 현재 공급량
- L² : MTK/USDC 유동성 풀의 유동성(상수)
- P : 기준 토큰 MTK의 가격
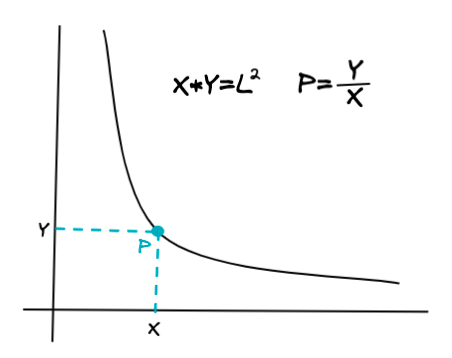
AMM의 CPMM의 원칙과 규칙에 따르면, 유동성풀에 제공되는 두 토큰의 공급량을 곱한 풀의 유동성(L²)는 상수입니다. 거래가 이뤄지는 동안 해당 변수는 항상 고정이며, 거래가 체결되는 양을 결정하는 요소입니다.
또한 MTK(My Token) 토큰을 기준으로 했을 때, MTK 토큰의 가격(P)는 Y/X로 결정되며, 유동성이 추가되거나 제거될때, 두 토큰의 비율을 결정하는 요소입니다.
CPMM의 가장 큰 단점인 높은 슬리피지로 인해 사용자들이 그 손해를 감당해야 하는 공식이었습니다. 이런 문제의 발생 원인은, 수학적으로 가격의 범위(Range)가 없기 때문입니다. 즉, 토큰 가격은 0이 되지 않고 무한으로 높아지고, 무한으로 낮아지기 때문입니다.

- Pa : MTK/USDC 유동성 풀에 제공하는 MTK의 최소 가격(기준 토큰 MTK)
- Pb : MTK/USDC 유동성 풀에 제공하는 MTK의 최대 가격(기준 토큰 MTK)
유니스왑 V3의 집중화된 유동성은 이런 단점을 보완하기 위해, CPMM의 원칙과 규칙을 벗어나지 않으면서 유동성 제공자가 직접 제공하는 가격 범위를 설정할 수 있게 업데이트했습니다. 이제 유동성 제공자는 가격 범위[0,∞] 내에 설정이 가능합니다.
V2에서 V3로 변화하는 과정에서 중요한 건, 기존의 CPMM 알고리즘의 원칙과 규칙에서 벗어나지 않은 업데이트를 해야 합니다.
그렇지 않으면 두 토큰의 거래량과 가격을 결정하는 유동성의 값이 변하게 되고, 암호화폐 시장의 가격에 비합리적으로 영향을 줄 수 있기 때문입니다.
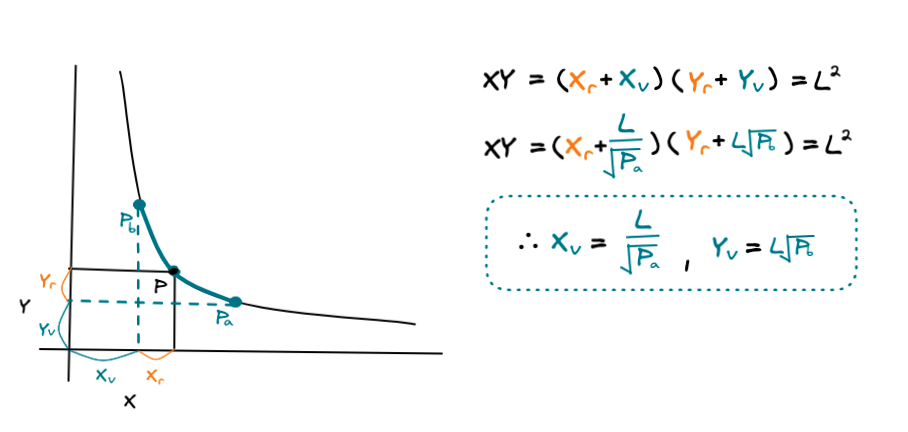
- Xr : MTK/USDC 유동성 풀의 실제의 MTK 총 공급량
- Yr : MTK/USDC 유동성 풀의 실제의 USDC 총 공급량
- Xv : MTK/USDC 유동성 풀의 가상의 MTK 총 공급량
- Yv : MTK/USDC 유동성 풀의 가상의 USDC 총 공급량
때문에 유니스왑 V3는 기존의 CPMM의 결과에 영향을 주지 않고 유동성 제공자가 가격 범위[0,∞]를
가상 공급량과 실제 공급량을 CPMM에 도입했습니다.
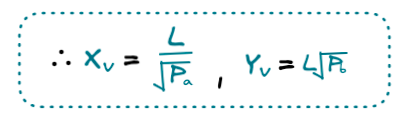
결론적으로 위와 같은 공식을 통해 가상의 공급량을 계산한 후, 실제 공급량을 계산하는 방식의 수학적 알고리즘을 도입하였습니다.
🔎 집중화된 유동성의 수학적 증명은 이해를 위해 가상 공급량 그래프(Curve of Virtual Reserve) & 실제 공급량 그래프(Curve of Real Reserve) 설명 후, 마지막 목차에서 알아보겠습니다.
(2) 가상 공급량 그래프(Curve of Virtual Reserve) & 실제 공급량 그래프(Curve of Real Reserve)
Example
- X : MTK/USDC 유동성 풀의 MTK 현재 공급량
- Y : MTK/USDC 유동성 풀의 USDC 현재 공급량
- Pa : MTK/USDC 유동성 풀에 제공하는 MTK의 최소 가격(기준 토큰 MTK)
- Pb : MTK/USDC 유동성 풀에 제공하는 MTK의 최대 가격(기준 토큰 MTK)
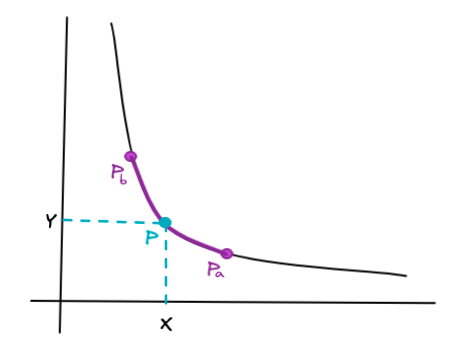
아까와 같은 예시로, 현재 MTK/USDC 유동성 풀에 가격 범위 [Pa, Pb] 내에서 유동성을 추가적으로 제공하려고 합니다.
이때, 유동성 제공자는 정해진 가격 범위에 따라 계산된 실제 공급량을 유동성에 추가해야 합니다. 이를 계산하기 위해 유니스왑 V3는
현재 토큰의 가격이 가격범위 [Pa, Pb]에 도달했다는 가정으로 가상의 유동성을 계산합니다.
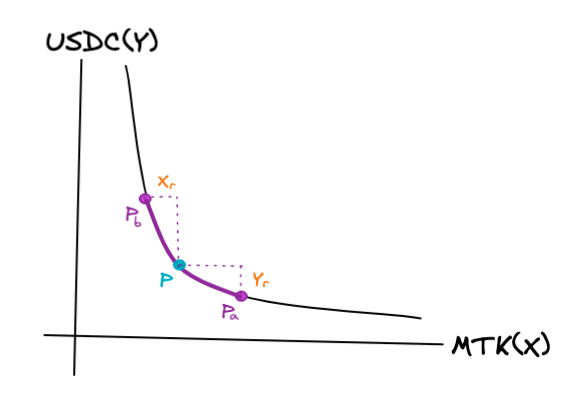
현재 MTK/USDC 유동성 풀의 MTK 토큰의 가격이 Pa와 Pb에 도달했다고 가정해 보겠습니다.
유동성 풀에 MTK(X) 토큰이 추가가 되고, USDC(Y) 토큰이 감소가 될 경우, 원래 가격 P에서 가격 Pa로 내려가게 됩니다.
유동성 풀에 MTK(X)토큰이 감소가 되고, USDC(Y) 토큰이 추가가 될 경우, 원래 가격 P에서 가격 Pb로 올라가게 됩니다.
이때 우리가 집중해야 하는 부분은 감소하는 토큰입니다.
유저가 유동성 풀에서 거래를 할 때, 유저가 갖고 있는 토큰을 유동성 풀에 추가하고, CPMM의 공식에 따라 체결된 토큰을 유저에게 제공하게 됩니다.
유동성 공급자는 유저에게 제공하는 토큰을 공급하는 사람입니다. 즉, 실제 공급량은 가격 범위[Pa, Pb] 내에서 거래하는 유저에게 제공되는 토큰의 양과 같습니다.
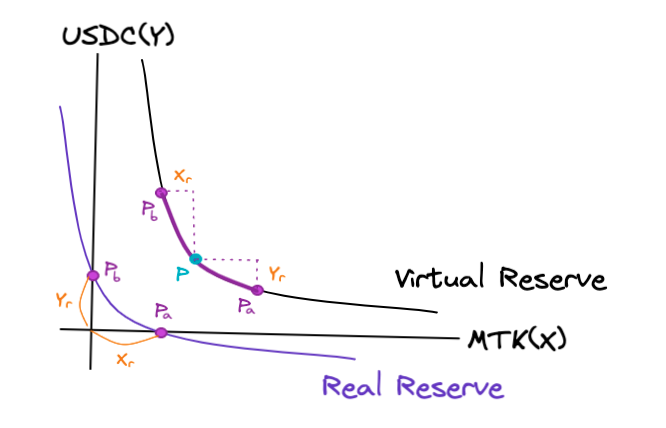
유니스왑 V3는 유동성 공급자가 설정한 가격 범위 밖에서 거래가 이뤄질 경우, 유동성을 제공하지 않지 않습니다. 이는, 유동성 제공자의 보상인 수수료를 받지 못한다는 걸 의미합니다.
위와 같은 가격 범위 [Pa, Pb]를 가상 공급량 그래프(Curve of Virtual Reserve)에 대입하여
실제 공급량을 통해 실제 공급량 그래프(Curve of Real Reserve)를 알아볼 수 있었습니다. 즉, 실제 공급량 그래프가 유니스왑 V3를 이용하는 유동성 공급자가 갖게 될 AMM 그래프가 됩니다.
(3) Uniswap V3 집중화된 유동성 수학적 증명
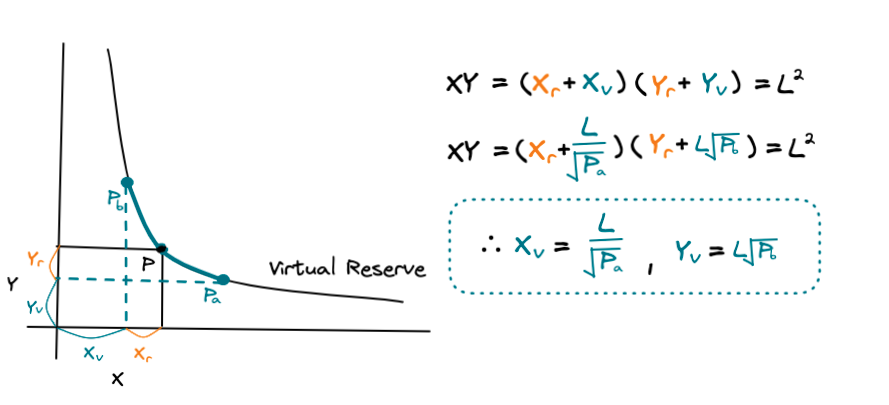
위에서 설명드렸듯이, 유니스왑 V3의 유동성은 가상 공급 그래프에 유동성 공급자가 설정한 가격범위[Pa, Pb]를 대입하여 가상 공급량과 실제 공급량을 계산합니다.
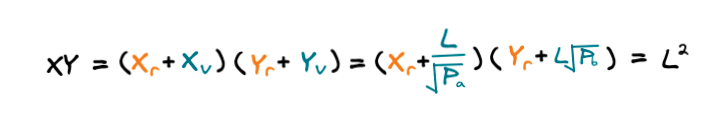
유니스왑 V3의 White paper에서 주장하는 AMM을 구현하는 합리적인 CPMM 공식입니다. 지금부터 이 공식이 수학적으로 합리적인 유동성 계산 공식인지 증명해 보겠습니다.
집중화된 유동성 공식을 증명하기 전, 실제 CPMM에서 주장하는 토큰 공급량과 유동성, 그리고 토큰 가격의 상호 관계를 알아야 합니다.
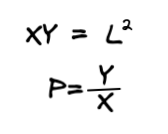
CPMM의 공식은 X * Y = K입니다. 여기서 X와 Y는 유동성 풀에 묶인 두 가지 자산의 총공급량을 뜻합니다. L²는 CPMM의 가장 중요한 역할을 하며, 두 자산의 공급량을 곱하여 결정된 상수 값으로, 특정 상황 외에 절때 변하지 않는 값입니다.
CPMM의 공식 X * Y = K에서, X와 Y를 통해 X의 자산가격이 결정됩니다. 유동성 풀에 제공된 두 자산의 가격(P)은 두 자산의 공급량을 나눠 계산됩니다(X/Y).
Derive Value X
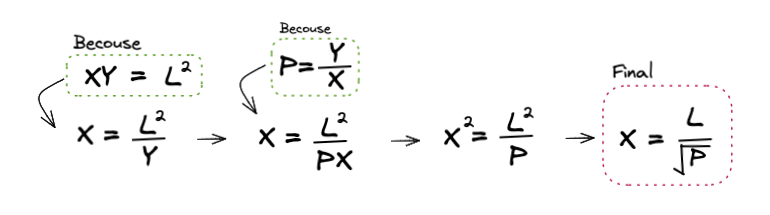
Derive Value Y
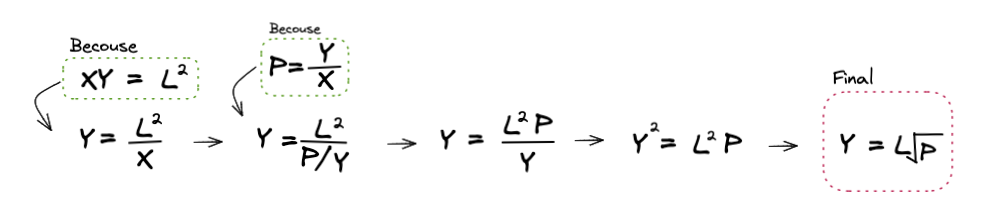
Final Derive
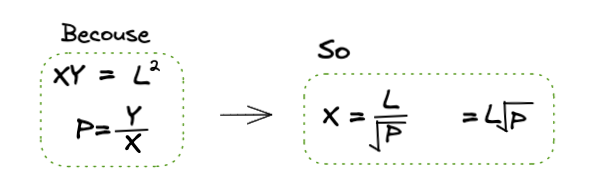
결론적으로 CPMM의 공식으로 최종 정의(Final Derive)를 위와 같은 증명으로 알 수 있습니다. 이제 위에 나온 공식을 사용하여 가상 공급량(Xv, Xy)을 정의할 수 있습니다.

위에서 언급했지만, 다시 말씀드리자면 유니스왑 V3가 주장하는 집중화된 유동성은 가상 공급량을 통해 기존의 CPMM 공식의 원칙을 지킨다고 했습니다. 최종적으로 유동성을 구하기 위해선 실제 공급량 + 가상 공급량을 알아야 합니다. 지금부터 가상 공급량을 수학적으로 정의해보겠습니다.
Derive virtual reserve of Xv
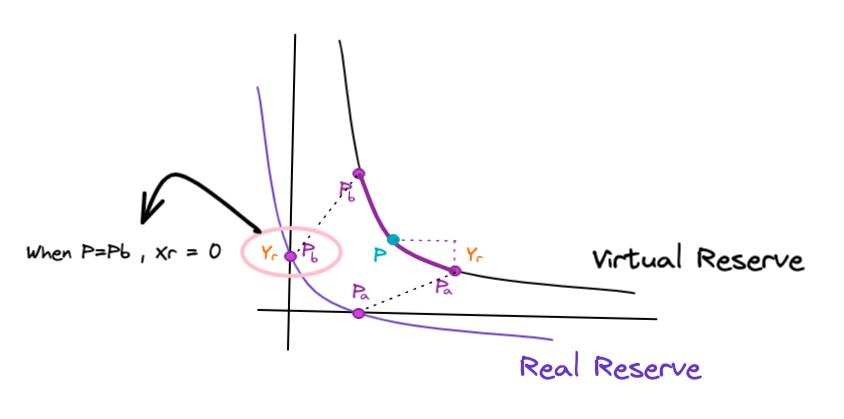
저희는 목차(2) 가상 공급량 그래프(Curve of Virtual Reserve) &실제 공급량 그래프(Curve of Real Reserve)에서
가격 범위[Pa, Pb]를 가상의 그래프에 대입시켜 실제 그래프를 구현했습니다. 그리고 실제 그래프가 유동성 공급자가 얻게 되는 유동성입니다. 이때 원래 가격(P)가 범위 최대 가격(Pb)가 됬다고 가정하면, 실제 그래프에서 가격 Pb에 도달하면 유동성을 더 이상 제공 할 수 없는 상태이기에, X 토큰의 실제 공급량(Xr)은 0 이 됩니다.
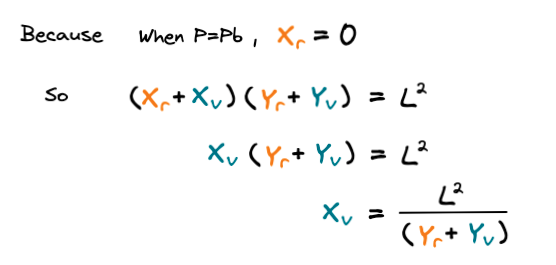
실제 그래프에서 가격 Pb에 도달하면 X 토큰의 실제 공급량(Xr)은 0이 되는 전제 조건을 이용하면 위와 같은 가상의 X 토큰 공급량(Xv)을 정의할 수 있습니다.
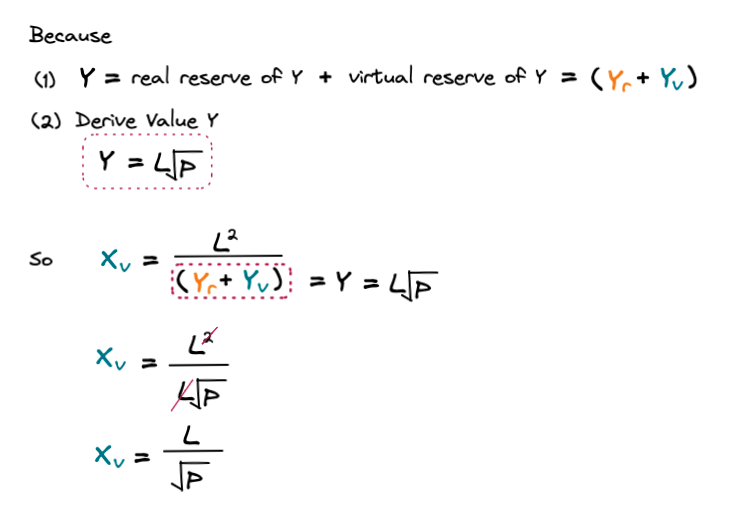
다음으로 위에서 정의했던 Derive Value Y와 실제 공급량 + 가상 공급량을 통해 위와 같이 X토큰의 가상 공급량(Xv)을 정의할 수 있습니다.
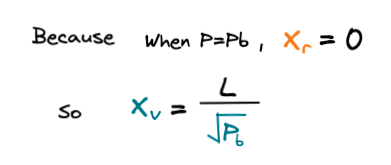
마지막으로 가상의 유동성 그래프에서 설정한 현재 가격(P)이 범위 설정 최대 가격(Pb)이 됐을 때라는 전제 조건을 대입하면 최종적으로
위와 같은 X토큰의 가상 공급량을 정의할 수 있습니다.
Derive virtual reserve of Yv
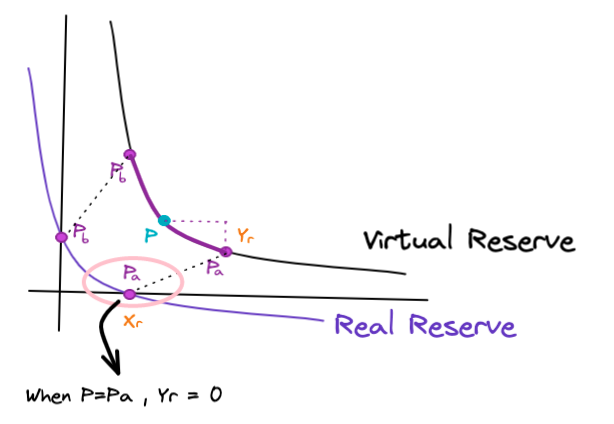
Y토큰의 가상 공급량(Yv) 토한 목차(2) 가상 공급량 그래프(Curve of Virtual Reserve) &실제 공급량 그래프(Curve of Real Reserve)에서 가격 범위[Pa, Pb]를 가상의 그래프에 대입시켜 실제 그래프를 구현했습니다.
이때 원래 가격(P)가 범위 최소 가격(Pa)가 됐다고 가정하면, 실제 그래프에서 가격 Pa에 도달하면 유동성을 더 이상 제공 할 수 없는 상태이기에, Y 토큰의 실제 공급량(Yr)은 0 이 됩니다.
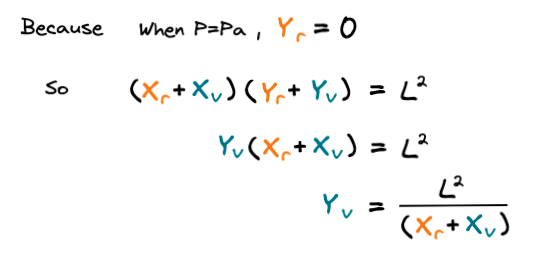
실제 그래프에서 가격 Pa에 도달하면 Y 토큰의 실제 공급량(Yr)은 0이 되는 전제 조건을 이용하면 위와 같은 가상의 Y 토큰 공급량(Yv)을 정의할 수 있습니다.
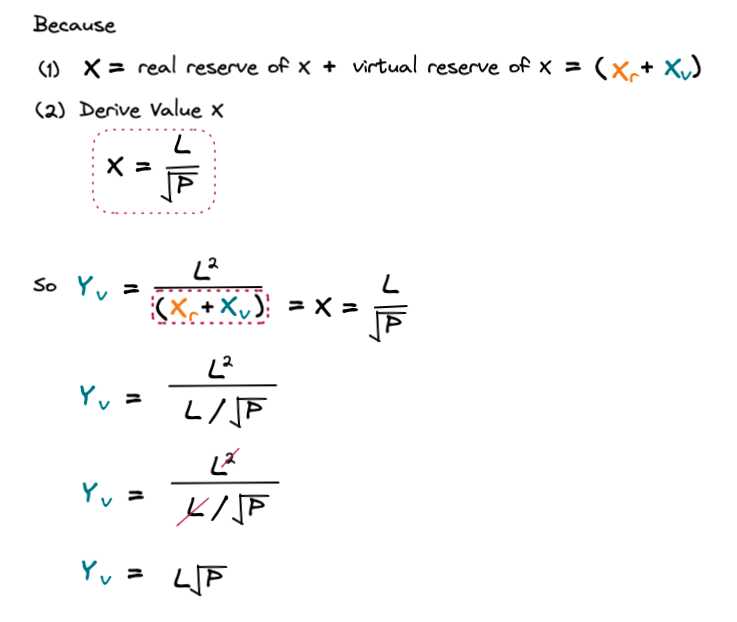
다음으로 위에서 정의했던 Derive Value X와 실제 공급량 + 가상 공급량을 통해 위와 같이 Y토큰의 가상 공급량(Yv)을 정의할 수 있습니다.
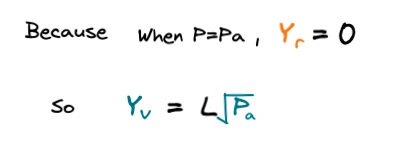
마지막으로 가상의 유동성 그래프에서 설정한 현재 가격(P)이 범위 설정 최소 가격(Pa)이 됐을 때라는 전제 조건을 대입하면 최종적으로
위와 같은 Y토큰의 가상 공급량을 정의할 수 있습니다.
Derive Final Real Liquidity
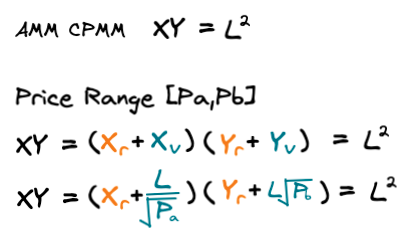
V2에서 V3로 변화하는 과정에서 중요한 건, 기존의 CPMM 알고리즘의 원칙과 규칙에서 벗어나지 않은 업데이트를 해야 합니다.
유니스왑 V3는 가격 범위 [Pa, Pb] 변수를 추가한 새로운 유동성 공식으로 업데이트가 되었습니다. 해당 공식이 기존의 CPMM X * Y = L² 공식에서 벗어나지 않는다는 걸 검증해야 했습니다. 그리고 위와 같은 일련의 증명으로 새로운 공식을 정의할 수 있고, 합리적으로 알고리즘으로 업데이트가 되었다는 사실을 알 수 있었습니다.
지금까지 DeFi Series는 Uniswap V3 업데이트의 핵심 집중화된 유동성(Concentrated Liquidity)에 대한 수학적 증명에 대한 내용이었습니다.
감사합니다.




댓글