
안녕하세요. 스마트컨트렉트 개발자 개발이 체질의 최원혁입니다.
저번 'Staking Reward 컨트렉트 파헤치기 (1)' 게시글에서는 스테이킹의 기본 설명과 알고리즘 공식 기본편에 대해 다뤘습니다. 아직 보지 않으신 분들은 아래 링크를 통해 먼저 학습한 후, 이번 게시글을 읽어주시기 바랍니다.
[DeFi Series] Staking Reward 컨트렉트 파헤치기 || Math | Algorithm || (1)
안녕하세요. 스마트컨트렉트 개발자 개발이 체질의 최원혁입니다. 이번 게시글에서 소개해드릴 지분증명에 의한 스테이킹(Staking) 리워드(Reward) Smart Contract입니다. 스테이킹 리워드 컨트랙트는
borntodevelop.tistory.com
추가적으로, 기본적인 알고리즘 공식을 Solidity로 구현하면 Smart Contract의 특성상 가스비가 크게 발생하는 치명적인 약점이 존재한다는 사실도 설명 드렸습니다.
이번 게시글에서는 이더리움 초창기 Synthetix dApp에서 사용한 약점을 보완할 수 있는 개선된 스테이킹 알고리즘 공식 심화편에 대해 알아보겠습니다.
스테이킹 알고리즘 공식 기본 편 개념 복습 :
🧐 지금부터 다루는 수학 공식은 수열의 합 시그마를 사용하여 정의됩니다.
먼저 공식에 사용되는 변수를 다시 정의하겠습니다.
- Si : i일에 유저가 예치한 토큰의 양
- Ti : i일에 컨트렉트에 총 예치된 토큰의 양
- R : 하루에 지급되는 보상률(Total amount of reward during the period / Staking Period)
- r(u,k,n) : 유저u가 k일 부터 n일 까지 예치하여 받는 보상 금액

위 공식은 유저가 예치한 토큰의 지분(Si/Ti)에 따라 k~n기간 동안 받는 리워드를 모두 더한 r을 구하는 공식입니다.
이를 활용하면 총 스테이킹 수량(T)에 변동이 있을 때마다, 기존에 스테이킹했던 유저들의 보상을 저장해야 하므로 반복문(for)을 통해 이미 예치한 모든 유저들의 보상 데이터를 다시 저장해야 했습니다. 이 과정에서 유저가 부담하는 가스비가 너무 많이 발생하기에, EVN기반의 Smart Contract 구조로 봤을때, 위와 같은 수학 공식은 매우 비효율적입니다. *해당 내용은 'Staking Reward 컨트렉트 파헤치기 (1)'을 보시면 이해할 수 있습니다.
스테이킹 알고리즘 공식 심화편 :

먼저 i일에 유저가 예치한 토큰의 양으로 정의된 Si을 다시 정의할 필요가 있습니다. 만약, 유저가 추가로 예치하거나, 인출을 하지 않는다면 k ~ n-1일까지 Si은 항상 같은 숫자인 공통된 상수임으로 수열의 합 규칙에 따라 밖으로 뺄수 있습니다.
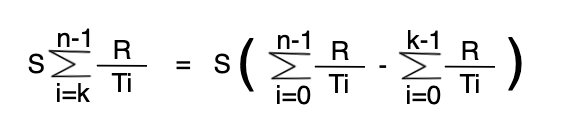
(1)에서 정의한 공식을, 수열의 합에 따라 (2)와 같이 확장시킬 수 있습니다.

스테이킹 컨트렉트가 만들어진 시점이 0이라 했을 때, k ~ n-1 은 유저가 스테이킹한 범위입니다. 때문에 (0 ~ n-1) -(0 ~ k)범위를 빼면 (k ~ n-1)와 같은 범위가 됩니다. 이러한 이유로 (2)공식을 증명할 수 있습니다.

기존에 있던 공식을 확장하여 사용하여 Solidity에서 사용될 공동 변수를 찾을 수 있습니다. 이를 통해 기존 공식에서 발생한 모든 유저의 상태변수를 변경해야하는 로직 대신, 공통 상태 변수만 변경하여 모두에게 반영할 수 있습니다.
우리는 (2)를 통해 공식을 확장시켜 두가지 새로운 변수를 만들어 냈습니다.
- 스테이킹한 토큰 당, 받게되는 리워드의 양
- 스테이킹한 토큰 당, 이미 다른 유저에게 지급된 리워드의 양
기존에는 특정 유저가 스테이킹한 양(Si)과 총 스테이킹된 양(Ti)를 이용하여 리워드의 양을 계산했지만, (2)의 확장된 공식을 통해 모든 유저에게 적용될 "스테이킹한 토큰 당"을 구할 수 있었습니다.
나중에 Solidity로 해당 알고리즘을 개발할 때 설명하겠지만, 스테이킹한 토큰 당 받게 되는 리워드의 양은 총 스테이킹의 금액이 달라질 때마다 바뀌는 공통 변수입니다. 또한, 스테이킹한 토큰 당 이미 다른 유저에게 지급된 리워드의 양은 각 유저의 주소로 매핑된 상태 변수에 저장되어 입금하거나 인출할 때 변경될 상태 변수입니다.
그리고, 확장을 통해 얻은 두가지 상태변수 공식을 쫌더 효율적이게 새로운 형태로 정의할 수 있습니다.
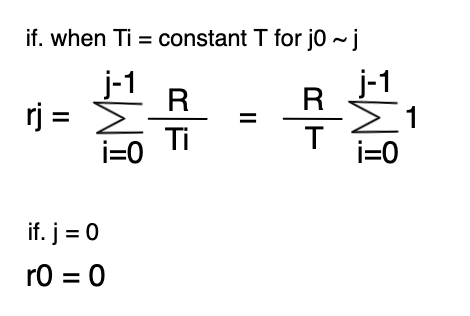
Ti는 i일에 컨트렉트에 총 예치된 양입니다. 이 값은 다른 유저가 추가로 입금하거나 출금하는게 아니면 변하지 않는 값입니다. 때문에 다른 유저가 추가로 입금하거나 출금하면 변하는 조건이 추가됩니다. 조건에 따라 T의 값이 변하는게 아니라면, 위와 같이 공식을 재정의할 수 있습니다.
j0과 j가 T의 값이 변하는 시점이라면, j0~j는 위와 같은 공식을 성립할 수 있습니다. 또한, j=0이라면 하루가 지나야 리워드가 지급되는 스테이킹의 원칙 상 결과는 0이 됩니다.
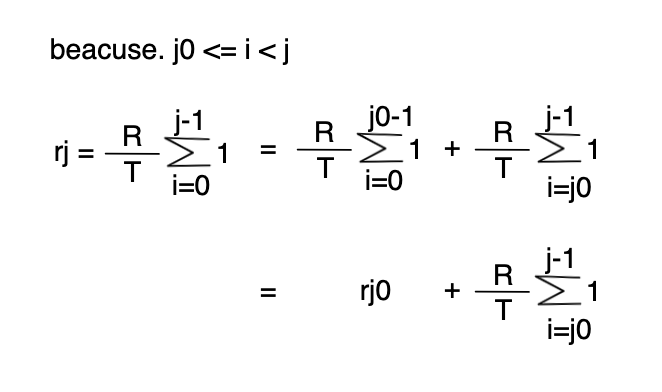
여기서 (3) 처럼 수열의 합 범위를 통해 다시 (6)처럼 공식을 확장시켜 다시 정의할 수 있습니다. 중요한건 j0과 j는 T의 값이 변하는 시점이며, T가 변하지 않는 j0 ~ j동안의 리워드 rj를 구하는 공식으로 다시 정의한 것입니다.
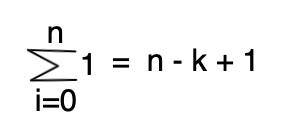
여기서, 새로운 개념이 등장합니다. 위 공식은 스테이킹 알고리즘 공식과 관련은 없지만, 적용시킬수 있는 공식중 하나입니다. 먼저 (6)를 증명한 후, 스테이킹 알고리즘에 적용시켜 보겠습니다.
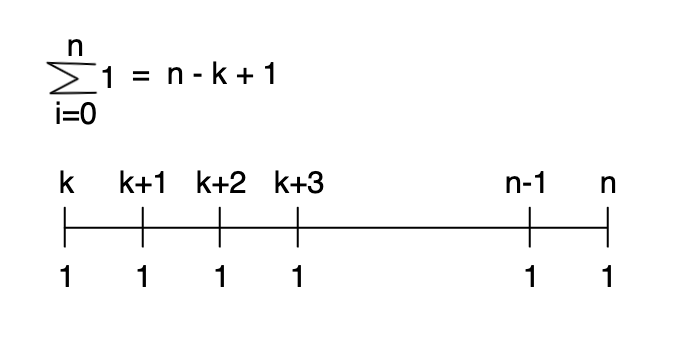
위 공식을, 보기 편하게 그래프로 표현하면 (8)처럼 나타낼 수 있습니다.
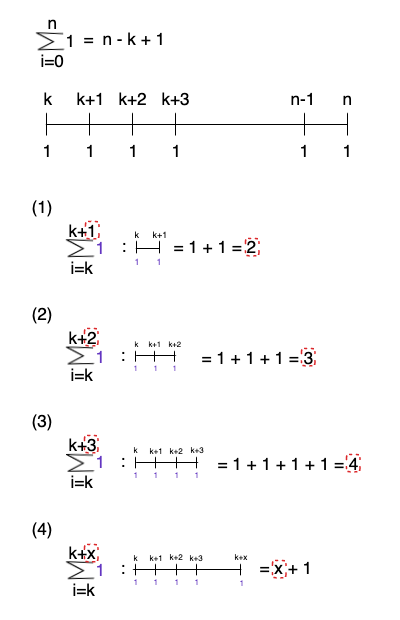
위 내용을 통해, 만약 n항이 규칙적으로 증가하는 k+x의 형태라면, 위 시그마 공식의 결과는 x+1이라는 것을 증명 할 수 있습니다.
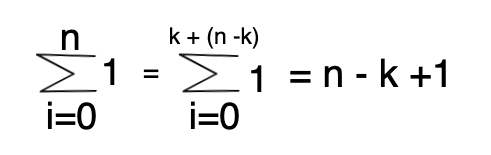
이를 활용하여 (7)을 재정의 하면 공식을 증명할 수 있습니다.
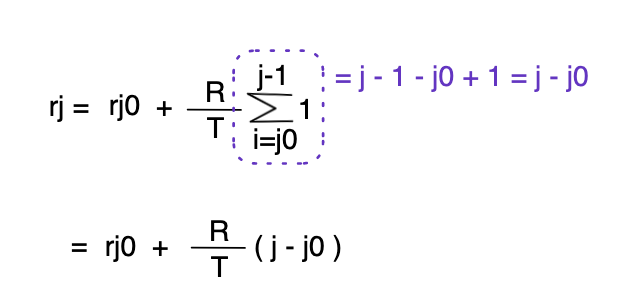
이제 증면된 (7)을 (6)에 적용하면, (10)으로 다시 정의할 수 있습니다.
example
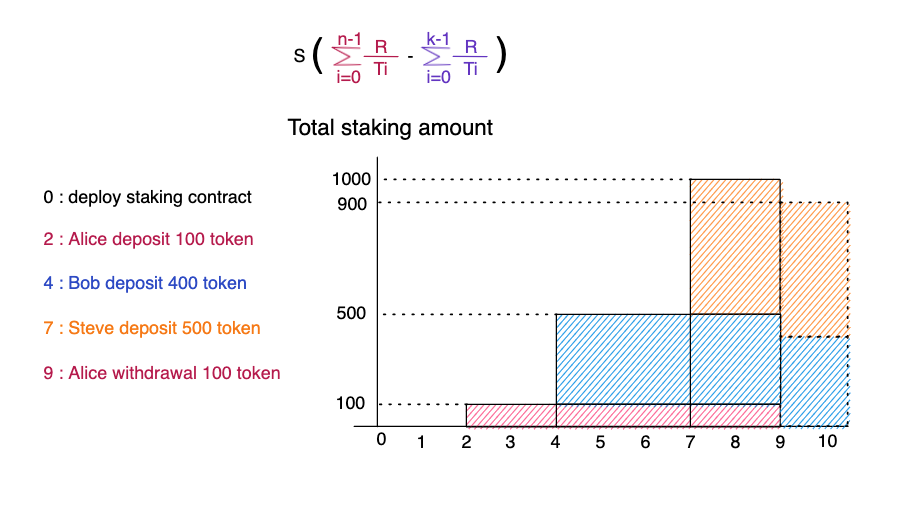
이제 저희는 전 게시글에서 다뤘던 예시 상황을 지금까지 정의하고 정리한 내용을 통해 다시 리워드를 계산해보겠습니다.
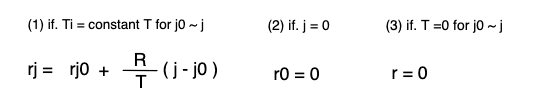
우리는 (5)에서 얘기했던것 처럼 T는 다른 유저가 추가로 입금하거나 출금하는게 아니면 변하지 않는 값입니다. 때문에 T의 값이 변하지 않는다면 j0 ~ j까지의 리워드는 (12) 공식을 통해 계산할 수 있습니다. 단, 만약 j0~j동안 T의 값이 0이면 아무도 스테이킹 컨트렉트에 예치한것이 아니기에, 보상은 0이 됩니다.
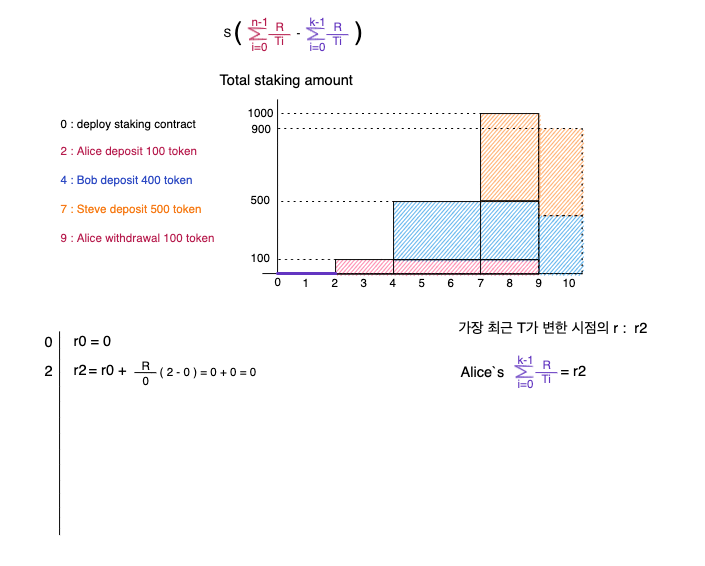
먼저 Alice가 100 토큰을 예치하게 되면, 이미 다른 유저에게 지급된 리워드의 양(r2)를 Alice의 주소로 저장하고, 가장 최근 T가 변한 시점의 r을 저장합니다. 이때 보라색 범위 r7 = (0~2)는 (12)공식에 의해 계산됩니다.
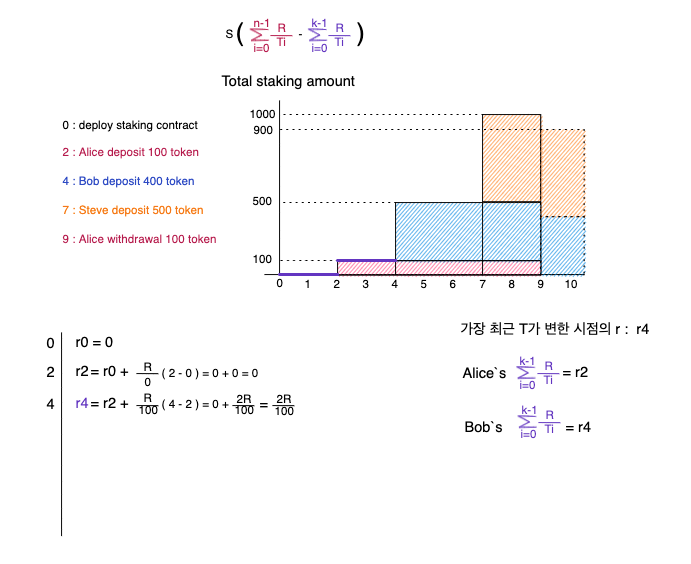
그 다음 Bob이 400 토큰을 예치하게 됩니다. 이미 다른 유저에게 지급된 리워드의 양(r4)를Bob의 주소로 저장하고, 가장 최근 T가 변한 시점의 r을 저장합니다. 이때 보라색 범위 r7 = (0~2) + (2~4)는 (12)공식에 의해 계산됩니다.
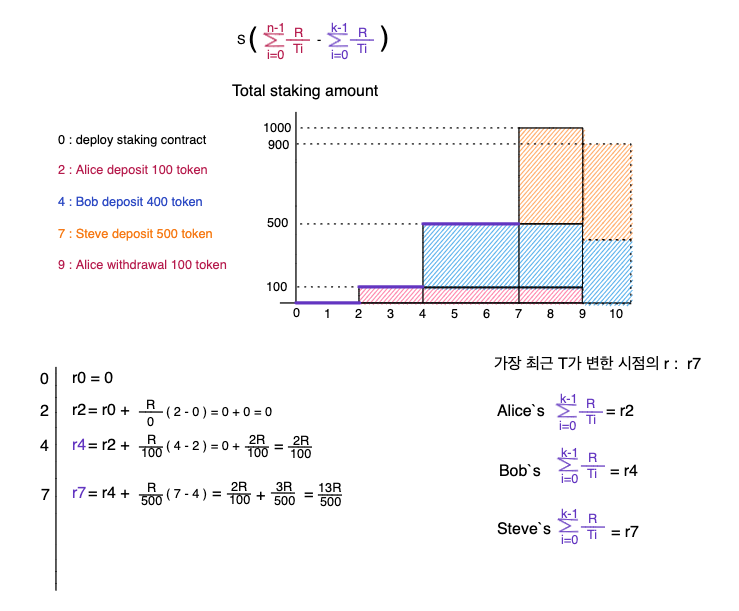
그 다음 Steve이 500 토큰을 예치하게 됩니다. 이미 다른 유저에게 지급된 리워드의 양(r7)를 Steve의 주소로 저장하고, 가장 최근 T가 변한 시점의 r을 저장합니다. 이때 보라색 범위 r7 = (0~2) + (2~4) + (4~7)는 (12)공식에 의해 계산됩니다.
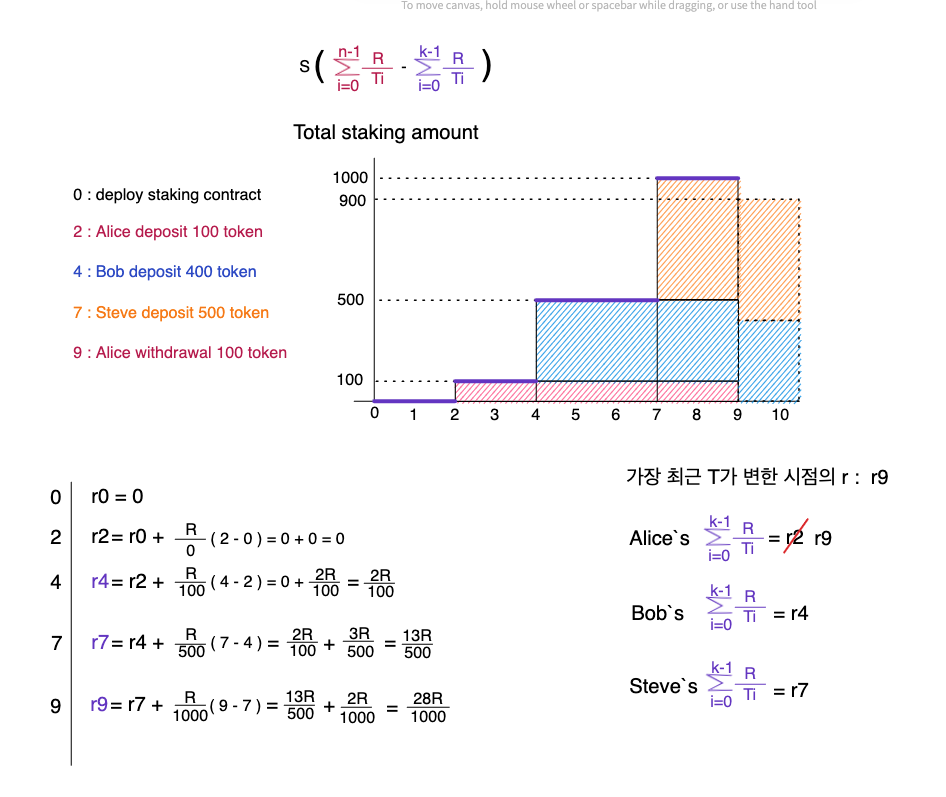
9일째 되는날, Alice가 예치(deposit)했던 100토큰을 인출(withdrawal)합니다. 저장되는 과정은 우선 같습니다. 이미 다른 유저에게 지급된 리워드의 양(r9)를 Alice의 주소로 저장하고, 가장 최근 T가 변한 시점의 r을 저장합니다. 이때 보라색 범위 r9 = (0~2) + (2~4) + (4~7) + (7~9)는 (12)공식에 의해 계산됩니다.
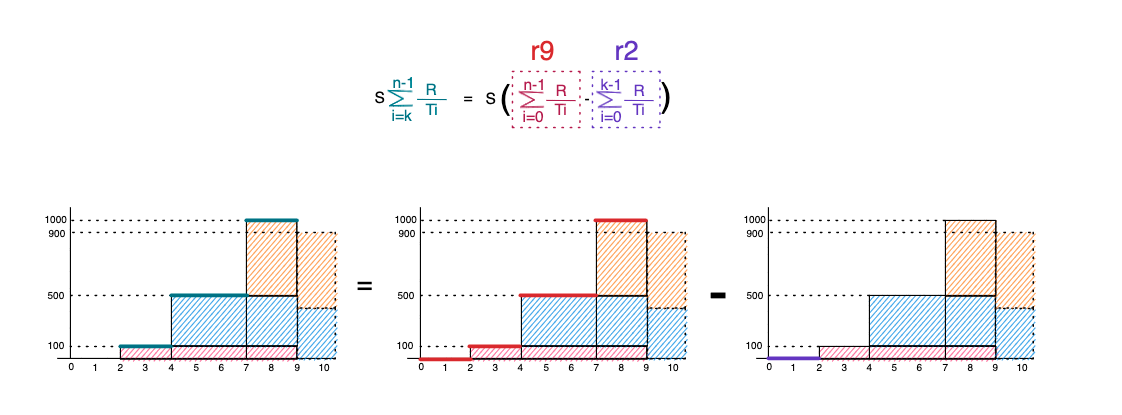
우리는 Alice가 100토큰을 예치할때, Alice의 지갑주소로 r2를 저장했습니다. 그리고, Alice가 인출하는 순간 우리는 r9를 구할 수 있었습니다. 그래프의 범위를 보면 초록색(2~9)가 Alice가 받아야할 보상이며, 우린 그걸 빨간색 범위 r9(2~9) - 보라색 범위 r2(0-2)로 공식을 증명하여 구할 수 있었습니다.

최종적으로, 지금까지 정의한 공식과 증명한 내용을 토대로 Alice의 총 보상 금액을 구할 수 있게 되었습니다.
여기서 가장 중요한것은 "가장 최근 T가 변한 시점 r"을 저장하는 것입니다. 이렇게 되면 "유저가 예치한 순간 r"과 "가장 최근 T가 변한 시점 r" 두가지만 변수에 저장하면 유저의 보상양을 구할수 있으니, 이전 게시글에서 다뤘던 공식에 비하면 굉장히 효율적인 로직을 구현할 수 있습니다.
긴글 읽어주셔서 감사합니다.
다음 게시글에서는 스테이킹 알고리즘 Solidity로 구현하는 방법에 대해 알아보겠습니다.




댓글